How the Circular Model Works in Concrete Terms and Why It Is Superior to the Hierarchical One – The Example of the Ketogenic Diet
Just now a new publication of ours appeared in an online journal, in which we demonstrated how to implement the circular model of cognition in concrete terms [1]. The physicist Rainer Klement, who calculated the analysis and provided the example data, was in charge. I was able to inspire him with my idea that one gains more insight with a circular model of knowledge than with the traditional, hierarchical one of “evidence based medicine (EBM)”. The key to this could be the formalization made here, which adopts a Bayesian statistical approach. It sounds more complicated than it is.
Background and problem
The hierarchical model of EBM, the current mainstream model, assumes that randomised controlled trials, if possible with placebo control, provide the best available evidence on whether an intervention works or not. Implicitly, this sets internal validity, the methodological rigour and validity of a study, against external validity, the transferability, usefulness and generalisability of findings in practice. I have analysed these problems in the first three parts of my methodology (Part 1: Evidence, an Unreflected Battle Cry; Part 2: Hierarchy or a Circle of Evidence; Part 3: The Consequences of the Hierarchical and Circular Models).
In practice, this leads to systematic reviews and meta-analyses disregarding most of the data and often even saying that there is no scientific evidence. Therefore, medical guidelines or meta-analyses often contain recommendations that contradict clinical experience or do not take into account a lot of insights [2]. The problem, as we have analysed in other publications [3, 4] and presented in more detail in part 18 of the methodology blog, is that internal and external evidence are independent of each other. One cannot pretend that one is more important than the other or that one presupposes the other. They don’t. Rather, there are studies that maximize internal validity – randomized trials – and those that maximize external validity – all naturalistic studies.
Now, if you neglect naturalistic studies in favour of randomized ones, as it is being done at the moment, you risk generating extremely reliable knowledge, but knowledge that either has very limited applicability or that nobody cares about. This is why we have proposed the circular model, which does not favour any type of information or study, but assumes that all studies provide different types of information that are relevant to different questions and should therefore all be taken into account. Which is what happens in the circular model of evidence. Foremost, I think this is a plausible theoretical demand. But the question is: How can this be achieved in concrete terms?
We have now provided the key. With a concrete example of application in a controversial topic. The application of the circular model succeeds if one adopts a Bayesian formal analytic approach that allows studies to change our prior knowledge while giving different weight to different types of studies. The advantage of a Bayesian analysis is that it incorporates our prior knowledge, which is generated by different data, into the analysis. I have discussed this before in a post on methodology (Part 5: On the Relationship between Empiricism and Theory 1), so I will keep it short with a brief reminder.
Bayesian analysis
The Irish pastor Bayes had recognized, that we make decisions based on prior knowledge, which changes the more information we have. The analysis named after him asks: if I have certain prior knowledge, how strong must empirical knowledge be in one direction or another to change it? Or, in other words, if all the prior knowledge we have is taken into account, how strong is the influence of a particular study or experience? Bayesian analysis, then, unlike classical frequentist statistics, works with conditional probabilities. It formalizes prior knowledge as the so-called “prior probability” or initial probability, adds a new study result, and then asks how this new result changes this initial probability into the so-called “posterior probability” or final probability.
We humans are all Bayesians. For we have all had formal or informal experience. Science also implicitly takes a Bayesian approach. The prevailing world view, professional or scientific experience, they all shape an implicit initial probability on the basis of which all available data, new study results or experiences are interpreted and weighted. Bayesian analysis now simply formalizes this procedure, which we always adopt anyway.
Classical Fisherian or frequentist statistics imitates the special case, which never actually occurs, that we are completely undecided on a particular question because we have no prior knowledge whatsoever, the “prior probability”, or the initial probability is therefore 50:50 or ½. Only if this is the case is frequentist statistics actually applicable in the strict case, otherwise not. Wagenmakers and colleagues rightly pointed this out in the example of parapsychology [5]. However, this should not only apply to psychology, but in principle to all statistics, including the statistics with which clinical studies are evaluated.
We have just set up a circular synthesis model with the help of Bayesian statistics for an example that is being discussed very controversially at the moment. It’s about the ketogenic diet for high-grade glioma, a difficult-to-treat type of brain tumour with a very poor prognosis.
The clinical example: ketogenic diet for brain tumours
The term “ketogenic diet” refers to a diet that mimics fasting metabolism, simply put. I will spare the biochemical and physiological background now. They are set apart in the original publication and in another publication of ours, which is also available online [6]. When we fast, the body breaks down fat. In the process, short-chain fatty acids, so-called “ketone bodies”, are produced. Most of the body’s cells, including nerve cells, can produce energy from these ketone bodies. And the few that cannot are supplied with sugar, which is formed in the liver from lactate, glycerol or glucogenic amino acids. That is why we do not die or faint when we fast, but can keep it up for quite a long time. People who are not used to it easily fall into hypoglycaemia at first, but that is another story.
Anyway, the body can be well nourished in a fasting mode if it feeds on ketone bodies from its own reserves. Every night we do this without having to get up and spread a sandwich, so we don’t starve. The ketogenic diet now takes advantage of this, except that the body does not fall back on its own reserves, but on protein and fat supplied through food. The ketogenic diet is therefore a diet in which carbohydrates are largely avoided and nutrition is provided mainly through fat and protein intake and carbohydrates mainly in complex form (e.g. salad and vegetables). Such a diet has proven successful for some neurological diseases, such as epilepsy. However, it is also used for cancer [6, 7]. This is because most cancer cells depend on sugar, which they get directly from food, and cannot feed on ketone bodies. So the ketogenic diet is something of a food deprivation programme for cancer cells. It has been proven to work in many ways [7].
We have now chosen ketogenic diets for aggressive gliomas as an example because there is very little and insufficient information here, precisely in terms of the hierarchical model. This is because there are only three studies in humans and these are rather small, partly compared with complex other procedures or are only available as observational data, i.e. not coming from a randomized study. Therefore, a classical reviewer would conclude: there are no scientific findings. Therefore, the therapy cannot be recommended. But if you take the existing 17 animal experiments and the data from the human studies together and add the basic physiological considerations, which we cannot simply ignore, then the picture changes.
The analysis and the insight
If, as the circular model suggests, we take all the data, i.e. the 3 human studies and the 17 animal studies together, we come to a different conclusion. We can formalize different considerations in such an analysis. Here, for example, parameters are used for which assumptions have to be made, the effects of which can then be seen directly in sensitivity analyses. For example, we assumed parameters for how important mechanistic considerations are, i.e. the theoretical knowledge about how ketogenic diets affect gliomas. Then we put a parameter into the model that formalizes how uniform the effects are across certain classes of individuals – humans, mice, rats. Finally, we formalized beliefs, such as the sceptical belief that data from animals are not transferable to humans, or even the fundamentally sceptical belief that ketogenic diets are harmful. Finally, one can include other mechanistic considerations, namely the finding that ketogenic diets support other forms of therapy, such as radiation or chemotherapy, in that the diet weakens the tumour and makes it more susceptible to the radical stress of the therapy. If you had very different data from human medical trials – for example, large cohort studies, randomized trial and case-control studies – then you could have added parameters to control the weighting of each study.
All these parameters now influence how the individual studies are accounted for in an overall model and how the statement of the analysis is evaluated. I reproduce the results figure from the original publication here:
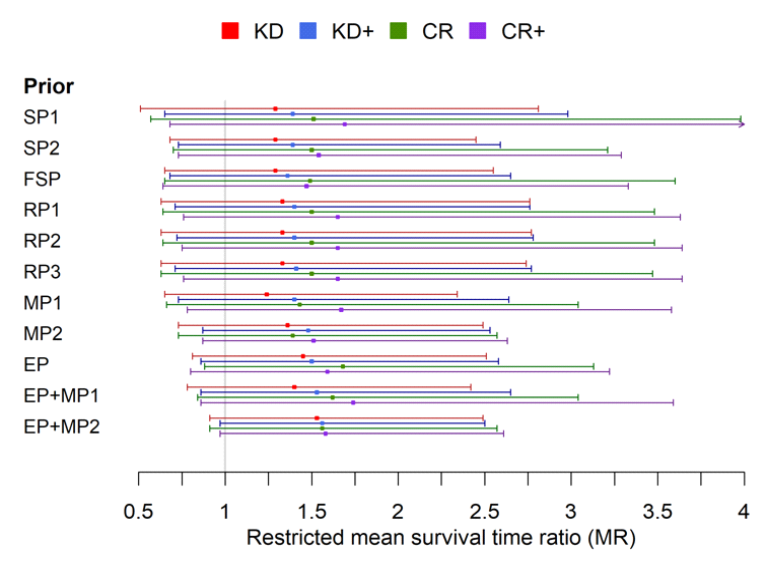
The most important insight from this analysis is probably that all the data indicate that a ketogenic diet confers a slight survival benefit. The estimates range from 1.2 to 1.5 on a ketogenic diet and from 1.5 to 1.7 on a caloric restriction diet with an add-on treatment. So those on a ketogenic diet are about 20-50% more likely to survive. Admittedly, none of these findings is certain in the strict sense, because the confidence interval in each case includes the line of indecision, 1, even if the most optimistic estimates already come close. But it is amazing how close together the estimates are, even when modelling sceptics, i.e. the sceptical priors (the first three lines in the figure). The fact that the findings are so widely scattered shows that there is still relatively little data available and the uncertainty is great. However, the fact that the estimation points are all relatively close to each other shows that all the data point in the same direction.
So the conclusion of our analysis would be: ketogenic diet and caloric restriction is definitely promising. The therapy promises to increase survival by 50%, and by 20% in the worst case, and should definitely be further investigated. Most importantly, we have shown that and how studies of different types can be combined in a formalized, quantitative analytical model.
Now, of course, we hope that the momentum will be taken up and that innovative minds in the Cochrane and EBM communities will set out to rethink their analytical strategies, perhaps adopt such a more circular strategy in a doubtful case, and stop throwing 95% of all data, whether mechanistic studies or cohort studies, overboard.
Sources and literature
- Klement, R. J., Bandyopadhyay, P. S., Champ, C. E., & Walach, H. (2018). Application of Bayesian evidence synthesis to modelling the effect of ketogenic therapy on survival of high grade glioma patients. Theoretical Biology and Medical Modelling, 15(12). https://tbiomed.biomedcentral.com/articles/10.1186/s12976-018-0084-y
- Klose, P., Kraft, K., Cramer, H., Lauche, R., Dobos, G., & Langhorst, J. (2014). Phytotherapie in den medizinischen S3 Leitlinien der Arbeitsgemeinschaft der Wissenschaftlichen Fachgesellschaften – eine systematische Übersichtsarbeit. Forschende Komplementärmedizin, 21, 388-400. https://www.karger.com/Article/FullText/370079
- Walach, H., Falkenberg, T., Fonnebo, V., Lewith, G., & Jonas, W. (2006). Circular instead of hierarchical – Methodological principles for the evaluation of complex interventions. BMC Medical Research Methodology, 6(29). https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/1471-2288-6-29
- Walach, H., & Loef, M. (2015). Using a matrix-analytical approach to synthesizing evidence solved incompatibility problem in the hierarchy of evidence. Journal of Clinical Epidemiology, 68, 1251-1260. https://www.ncbi.nlm.nih.gov/pubmed/26148834;
- Wagenmakers, E. J., Wetzels, R., Borsboom, D., & van der Maas, H. (2011). Why psychologists must change the way they analyze their data: The case of psi: Comment on Bem. Journal of Personality and Social Psychology, 100, 426–432.
- Jansen, N., & Walach, H. (2016). The development of tumours under a ketogenic diet in ssociation with the novel tumour marker TKTL1: A case series in general practice. Oncology Letters, 11, 584-592. https://www.spandidos-publications.com/10.3892/ol.2015.3923
- Klement, R. J. (2018). Fasting, fats, and physics: Combining ketogenic and radiation therapy against cancer. Complementary Medicine Research, 25, 102-113. https://www.karger.com/Article/FullText/484045
